Continual Learning
Our research in Continual Learning focuses on developing AI systems that can continuously acquire and refine knowledge over time without forgetting previously learned information. We utilize analytical learning approaches to create methods that efficiently adapt to new data while preserving existing capabilities.
We introduce a novel approach to class-incremental learning (CIL) that addresses the challenges of catastrophic forgetting and data privacy. The proposed Analytic Class-Incremental Learning (ACIL) framework allows for absolute memorization of past knowledge without storing historical data, thereby ensuring data privacy. We theoretically validate that ACIL can achieve results identical to traditional joint-learning methods while only using current data. Empirical results demonstrate that ACIL outperforms existing state-of-the-art methods, particularly in large-phase scenarios (e.g., 25 and 50 phases).
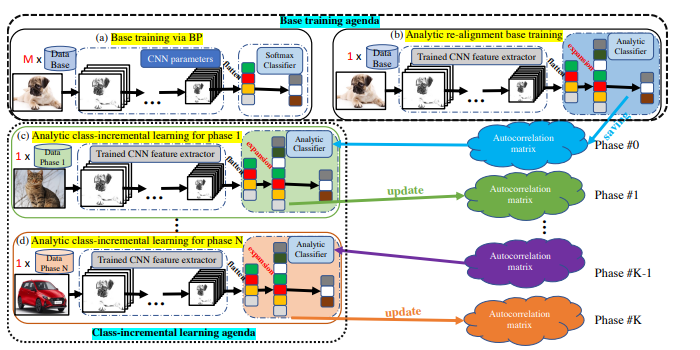
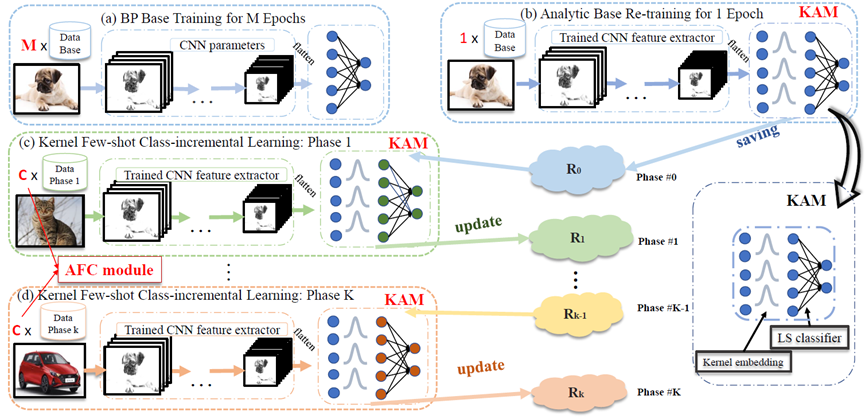
In this paper, we focus on few-shot class-incremental learning (FSCIL) and extend the analytic class-incremental learning (ACIL) to this realm. To tackle the few-shot issue, we propose the kernel analytic module with Gaussian kernels that conduct FSCIL in a recursive manner with analytic solutions, and the augmented feature concatenation module to balance the preference between old and new tasks. Our method demonstrates state-of-the-art performance on several datasets.
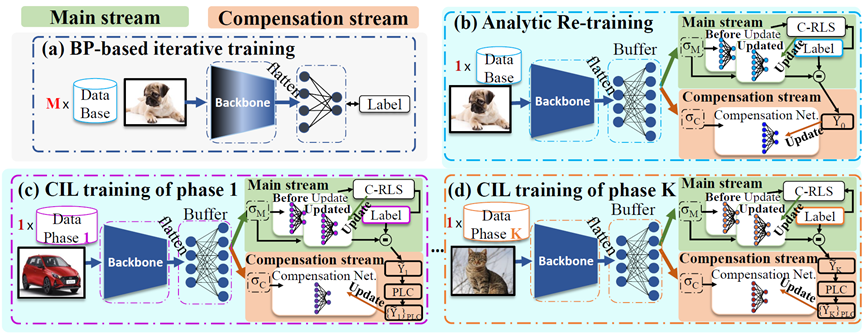
In this paper, we focus on the under-fitting issue of linear classifier used in analytic continual learning. To achieve better fitting performance, we propose a dual-stream structure for class-incremental learning. The main stream redefines the class-incremental learning (CIL) problem into a Concatenated Recursive Least Squares (C-RLS) task, allowing an equivalence between the CIL and its joint-learning counterpart. The compensation stream is governed by a Dual-Activation Compensation (DAC) module. This module re-activates the embedding with a different activation function from the main stream one, and seeks fitting compensation by projecting the embedding to the null space of the main stream's linear mapping. By introducing the dual-stream, our method achieves better fitting performance and performs improved results when compared with existing CIL methods.
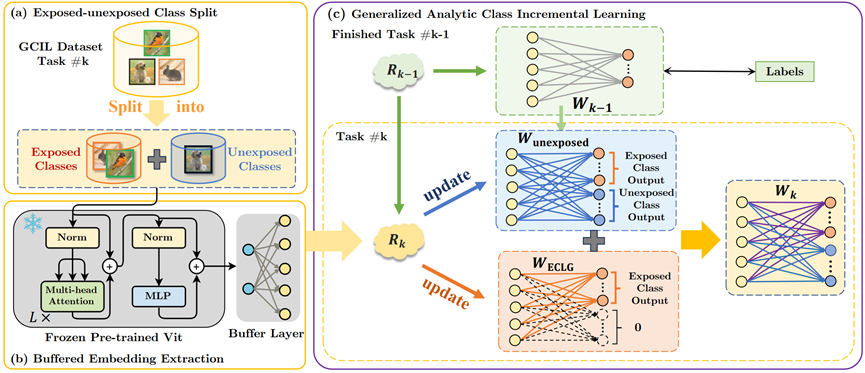
The generalized class-incremental learning (GCIL) aims to address the continual learning problem in a more real-world scenario, where incoming data have mixed data categories and unknown sample size distribution. In this paper, we propose a new exemplar-free GCIL technique named generalized analytic continual learning (GACL). The GACL extends analytic learning to the GCIL scenario. This solution is derived via decomposing the incoming data into exposed and unexposed classes, thereby attaining a weight-invariant property, a rare yet valuable property supporting an equivalence between incremental learning and its joint training. Such an equivalence is crucial in GCIL settings as data distributions among different tasks no longer pose challenges to adopting our GACL. Empirically, our GACL exhibits a consistently leading performance across various datasets and GCIL settings.
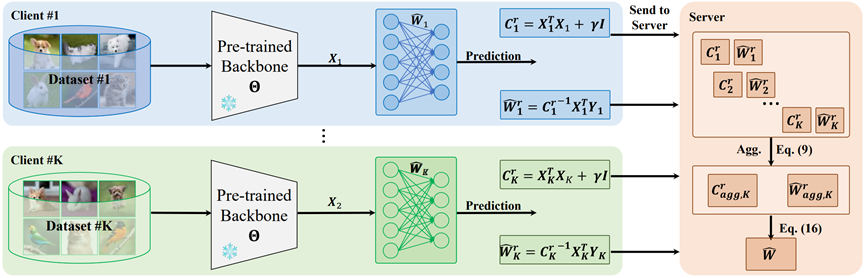
In this paper, we achieve the invariance to data partitioning in the realm of federated learning via a dual branch of utilization of analytic learning. Our AFL draws inspiration from analytic learning -- a gradient-free technique that trains neural networks with analytical solutions in one epoch. In the local client training stage, the AFL facilitates a one-epoch training, eliminating the necessity for multi-epoch updates. In the aggregation stage, we derive an absolute aggregation (AA) law. This AA law allows a single-round aggregation, reducing heavy communication overhead and achieving fast convergence by removing the need for multiple aggregation rounds. More importantly, the AFL exhibits a property that , meaning that regardless of how the full dataset is distributed among clients, the aggregated result remains identical. This could spawn various potentials, such as data heterogeneity invariance and client-number invariance. We conduct experiments across various FL settings including extremely non-IID ones, and scenarios with a large number of clients (e.g., ). In all these settings, our AFL constantly performs competitively.